05haut

[5a] ‘Violins and Cows’, Art-Language, Vol. 2, No. 4, June, 1974, pp. 1-25.

There is no point in looking for a well-formed art structuralism – or an ‘all-over’ methodologically unambiguous monotheoretical model of art. In the nineteenth century, the high degree of mechanistic systematicness in the sciences provided the grounds for the vaunting of specious autonomy theses. The currently prevalent aspiration to produce such a ‘structuralism’ is commensurate with the deterministic non-castellated model used by the nineteenth century art historian...

The point is to consider what we learn/share. Whilst not rejecting the notion out of hand, it seems that we do want a space more tractable than a Husserl-popularist ‘empathetic/ethical’ space. This desiderate seems to lead to transformations of spaces. It is required of the indices that they be rich enough to catch transformations in a given space and transformations of given spaces. The same index should support both intraspatial and interspatial transformations. Whatever we want to have, there is some point in looking diachronically for possible relations in such spaces. The interesting thing, however, is that we are dealing with transformations of ‘logical space’ – not just transformations in a logical space...

... Generalized notion of learning as the compactness of any reference point i, but is not the redundancy of localization (re-interpretation) so that xi ą xj ...

We can suggest a (still provisional) definition of an item searched by the Art & Language Index = def. a ($x)( $y)(x is a member of A & L and x learns a from y and x ą y). Here y may be a member of A & L in which case we would have y contributing to x’s A & L heritage (index-providing status) or y need not be in A & L.

An alternative definition which catches the notion of sharing (people might be happy about this) would be found in:

Searched by the index of = def. A & L (x) (if x is a member of A & L then (($y) x learns a from y and x ą y).

Now, it has already been pointed out that one of the features of our conversation (epistemic, etc. activity) is that some parts of it involve transformations of logical space, rather than merely transformations in a logical space. The former transformation is what the ‘(T)’ in the index is supposed to express. It is appropriate to consider the index/map as permitting certain sorts of idiomatic talk. What we want to do is search the ‘work’ we can get hold of in such a way that some of the modalities in the conversation might be revealed.

Metaphysical problems of indexing without iterated modalities

An impressionistic semantic model? But this doesn’t commit us to ultimately ‘reduce’ the citations, to the right hand side of the index, to psychology. For the left hand side the intra – and inter – set transformations are introduced as the (indexical) expressions of (a posteriori) facts of ideology. The generalizations out of, and into, a point of reference/proper name/possible world/an accessible fragment of the world is no more subject to a priori criteria of set consistency, compatibility and exhaustion than a pragmatic model a la Montague. That is, apart from ‘historical-dialectical’ (sic) arguments about the growth and development of indexing ... a ‘logic’ has to deal with the assumptions of complete/exhaustive descriptions (intensional-extensional) as wff (well formed formula) and providing a T-F mapping ® calculus that’s undecidable … We don’t have problems of the decision theory in indexing (ipso facto) – maybe that’s our last tautology... Anyway, mathematics (algebra) have their own scandals (to deal with) in their categorization of ‘nature’, and as nature; never mind the possibility of the trans-world-heir-lines (identity?) expressible with ‘(T)’ ... wff-ness and compactness of (the categories of) a point of reference is a MMiÎI situation. Axiomata are locked in a historical continuum just like any (±) mapping...

Now, one thing is that we can suggest a system of paranomic (this word is not altogether accidentally like ‘paranoiac’) modalities. What we mean by this, really, is that in our conversation we don’t want to make stronger modal claims than can be accommodated in an adjunct of the nomic context. Remember, we’re talking about what we learn; so, perhaps we’re dealing with modality interfaces. The modalities we are talking about subsist in the interfaces between alethic, boulomaic, deontic and evaluative modalities; this may seem pretty vague, but if you’ve done any work recently, try thinking about its Ordnuungscharakter. Anyway, it must be shown that the modalities an index might come up with are distinct from ‘logical ones’ – or maybe stronger logical ones. Maybe we have to consider both…

...An index set is seen as covering possibles. The necessities, or perhaps rules, apply to possibilities. But anyway, at this stage it might be argued that there is some way in which, as it were, the index set of any assertion involves the possible context of its application, or projection, or acceptance, etc.

There are some problems associated with the concepts of possible worlds, or possible individuals in terms of ontological status and identity. But ideological status is most use; the point is that we want to consider state-to-state transformations of context, etc. of what we and others have said.

...But really, faced with the elliptical situation of ‘interpretation’, we ought to shut up. This is the best way around the classical and orthodox objections to (non-orthodox) semantics (i.e. semantics as a (formal) theory of natural languages and as a formal language). However, a semantical aspect, or rather a ‘series’ of semantical aspects, seems to be reflected in our nature – that is, our natural language, our discourse and so on. And that is the absurdity of a sophisticated ideological ‘matrix’ (through and past Kripke and Hintikka) that denies any ideological point of reference. (Ideology may be thought of, in a radically atomic way, as submerged in ‘semantics’.) So, inasmuch as it would be paradoxical to say we have any problems, we’d better say ‘we have a few approximations to a solution of the reflexivity of language.’ Some suggestions for the quasi-solutions originally came from Abraham Robinson’s non-standard semantic-model theory as interpretations of formal syntactical languages by approaching a modal logic. But the question comes up what sort of modalities (alethic, etc.) and how many of them? This is the nexus point of semantics and indexes; the axes of an index can be seen as the parameters of a pragmatical approach to natural languages...

Or rather, we are faced with the – non-deontological (chronic) – ought of mapping if a parameter is not an approximation to a (highly generalizable) pragmatic situation ... The projectibility of a mapping has traditionally been the a priori weights attached to a complex (sic) inductive function. There is, however, a mutual dependence between the scalar and vector dimensions of a point of reference and its ‘logical’ transformations. Instead the values/shopping list of modalities of any fragment of (pre-) language provides an ordinal wave! Whither anaphor?

A point of reference – as an atomic element of the world – is methodologically intractable; there is a localizing anaesthesia however.

What are these individuals? These are presumably what seem to be referred to by the individual citations, that is, the citations to the right of the ‘original’ of a document list, are, or rather contain, a sort of reference to the merely possible individuals which add up or constitute elements of the (original) point(s) of reference commensurate with the left hand index element – so the statements interpreted from the citation list on the right may lack a truth value, but need not.

Another thing is that the index logic (i.e. interpretations, etc.) might (should) be free of existential assumptions. And anyway, some of the domains may be empty. Now, also, we need to sort out the problem of intensionality of modal contexts. The main ideal is to distinguish between modalities de dicto and de re – and show that names and definite descriptions behave differently in these contexts. The sentential-operator notion of modality (i.e. the de dicto) may be taken as basic and with the help of operators in common in propositional logic, de re modality is, or may be seen as, a special case of a more general kind of modality.

A basic idea in sorting out the logical modalities has been the idea that necessity is associated with ‘truth in all possible worlds’. Now, it seems that we want the index to provide some instrumentalities so that an analogous notion may be mobilized in the context of our conversation, and conversational aspiration. The fact that we do talk to each other has been increasingly an important concern.

Anyway, ‘world’ is a bit much. Usually, ‘point of reference’ is better. In Professor Carnap’s construction, the role of index (possible world) is filled by state descriptions. Now, it could be argued that what the index does contain is state descriptions; it would be best here to call them ‘histories’. A ‘state description’ characterizes completely a logically possible (conversational) state of affairs – not necessarily at one instant of time. It does this to the limit of its primitive predicate(s) and names. The histories might well do the same. The histories ‘describe’ the ‘basic’ possible facts. This doesn’t mean that non-modal ‘statements’ (index entries perhaps) formed solely in terms of non-analyzed (sufficiently clear) predicates and names don’t have modal implications – they do. And we could arrange for further such implications by putting restrictions on histories (and on later entities to be constructed) in the way that Professor Carnap put restrictions on ‘state descriptions’ by using meaning postulates. So a history, ‘(±) A123)’, etc., is a basic level of description in a syntactic sense – but, also, non-analyzed properties have a semantical and epistemological dimension. If the ‘histories’ are seen as representing alternative logically possible states of affairs, we might expect that a statement, or statement set, or string of interconnected sentences is paranomically a necessity, or, at least, has a certain ‘weight’ if and only if it holds all members of a subset of the set of histories where that subset is considered to ‘correspond’ to Art & Language discourse in some way.

We can’t always ‘internally’ systematize what kind of ‘necessity’ we mean; it’s our problem to get a lot of general regularities or not get them; it might be said that we deal with a cross-modal abstraction.

The histories in that subset represent the paranomically possible alternative histories. Other subsets represent other notions about what is paranomically possible, i. e. involve a transform out of the space. The other subset simply allows transformations in that space. It would be alright to call each such subset a reference point, and reference points represent theoretically (logically) possible determinations of what is paranomically possible.

... The (epistemo)logical products/problems of the index don’t raise the old criteria of adequacy solution of operationalism ... Funnily enough the history of the metaphysics might suggest we are dealing with nature (and directly). Rationality has (always) remained uninterpreted – uninterpretable – in the Hegelian equation: actual (world) = the rational. We have instead ‘actualization’. N.B. the vectoral assumptions are – or rather conditions – functions for the continuity of (an actualized) reality ... but even our rules/axiomata are dependent on memory (i.e. = revision). Natural necessity applies to possibility and counterfactuals don’t get into the index...

... There’s a difficulty; maybe we can’t any longer identify an alethic necessity with that which holds in every history. The reason is that there will no doubt be alethically necessary statements available from the index in which paranomic ones appear. But for paranomic statements we can’t give a criterion for holding in a history since the same history appears at different reference points (i.e. in subsets of the set of histories). Whether a statement is paranomically acceptable does not depend just on a given history, but on the alternatives to that history, i.e. on which reference point is being considered. What’s needed is a hierarchical. structure for alternative possibilities. As well as breakdowns of a simple reference theory to provide the meaning of ‘propositional attitudes’ (that is, where and how do you pick out your individuals in opaque areas?), we’ve got the problem of proliferation of possibilities concerning the actualized world. This point rests upon both the features of attitudes – which are planning, constructing and disagreeing – and the truth-value foundation (or primitives) of modalities, necessarily and possibly. In crude terms the problems are not only of realizations of different possibilities but an achievement to make a world which would match the real logical possibility and an ‘apparent’ (linguistical) possibility (cf. Hintikka). We could bring in essentialism, but this is suspect itself in the context of modalities. (It also makes the claims for opacity footless. But that would only occur in the dreams of a diachronic – worse, pure competence/non-performance … world of cyberneticians.) There is a weaker type of general essentialism, i.e. identity through the (unmapped-unmappable) modalities of non-difference – perhaps opacity is a bit much, despite the fact that indexically you are working-in-the-limit. The points of reference are not ersatz possible worlds in the index. Whatever historicity a set may have embedding, etc. – what it ‘tells us’ prevents indexes becoming objects of pure phenomenalistic contemplation.

(Historically it can be challenged that a (in a metamathematical or intuitional situation) the model of a formal system is the appropriate ordering of the procedure. For example, if this procedure were applied in function theory, in respect of consistency and completeness, it might lead to separate definitions of continuity for each function. This is a standard traditional problem of axiomatics, the interpretations of formal systems being isomorphic. So we don’t get, and shouldn’t expect, necessarily, standard models for interpretation. If we are in need of one definition of what constitutes a model of a given system we should not expect only one helpful answer (cf. ‘The Ontological Significance of the Lowenheim-Skolem Theorem’).)

...So when principles rather than mere facts about the conversation are considered, ‘reality’ (from the point of view of conversation) may correspond to point of reference R, with one of its histories representing the matters of fact, or to point of reference R1, with one of its histories representing the matters of fact; these are reference point structures. A sentence expressing ‘paranomic conversation’ necessity holds in a point of reference structure just if that which is deemed necessity holds in every point of reference structure R containing the same point of reference as R.

Redemption not Adaptation

We may have to deal with set membership as an affirmation. Certainly, we’ll have to cope with resonances along any wave-like parameter of conditionship. Set membership is not – cannot be – trivial ... neither can we accept any forgone conclusion over set membership ... the set can’t be thought to be ‘closed’ save as a point of reference ... in the margin of the index. Perhaps a point of reference is a path ... ideology/‘lived through’ and can’t have any identity (membership) criteria except with an iterated range of modalities – of that ideological point. Similarly as a point and not an atomic element, it operates as a function on a rational time dimension of belonging to a set (AL); this pseudo-reflexivity (Kaplan’s solution for paradoxes remains, for us, on the surface – and so a paradox resolved) is hybridity. But as that pseudo-reflexivity is non-paradoxical, via an iteration from a list of pragmatic aspects (of the work, the discourse, yourself), you have the possibility of sameness with respect to any subset of the ideology set ‘I’ – similarly with different sets embedded in ‘I’. Yet the depth vector/function of that reflexivity is unknown only iterated ... as a point of reference not a dynamic. With hybridization ‘sameness’, ( {i 1} = {i 2} ) may be a possibility, only through the necessity of a revitalized, revitalizing vector ... (H, H°, H°°, h°, h°°).

So we’re still left with the teleological problems – and they proliferate: ‘going-on’ moves us away from ‘grammar’ and ‘grammaticality’. ‘Why our system is not tautologicaily mystical’ ... ‘how it could not be possible to revise a system’ ... that would be a mysticism of a kind – of the kind that lets syntax (rules – conditionality – defence – completeness) in any formal mode remain ‘on the page’ in some way ... and thinking it gave (an undecidable) description of the world. Back to ‘what is a problem?’ Are our injunctions to the idols just brought about by a difference of macrosociological inputs of the world of art? (Remember the possibility of ‘=/ą’ above.) Pseudo-problems and problems: our categorization of a set (of sets) AL1 only partially excludes something in a funny sort of way. No, it doesn’t even do that ... N.B. ($x)M1(x),

where M = any modality from indifference to hatred to ... etc. Our set-inclusion belongs to a non – ‘semantics of natural languages’ mood of ideology. ‘Everything’ is included/indexical to the set AL – in one embedded or non-iterative way or another.

Is this adaptation? Is this the escape from determinism? (Ideology is fixed by determinism.) After all we still have our reports/indices. What quasi-structural principles can we get away with for ‘structure ą a closed system’? ... N.B. any structural items despite formal relations are resonant with each other ... i.e. {i = j} k/ {i ą j} 1, and provide the possibility of a generated set of same or different items ‘e IG1’, which includes as ‘same’ or ‘different’ all past items.

That’s what diachronic experience is –

Concatenata: they’re not words or the morphs of linguistics ... they’re a non-arbitrary detachment (whose depth we don’t know) of a body (I e AL1) discourse. The concatenata are (notoriously) ordinal – rationality is after the event – or an exhausted M IG1 (experience) and non-revisionary – or a tacit cardinality as a product of the vectors of going-on ... going-on as myth.

H is a dynamic set condition – characterizing unification. We can’t determine or even exhaustively map these conditions. Any concatenation is relative to any set conditionality – unsaturated. In the absence of a possible teleonomic set - (T) - any expression of identity is (say) the product of two functions such that T1= T2, you/we always ‘have a difference’.

The ‘same’ and ‘different’ situation is only accessible a posteriori.

When H is completed (on the form) you can go to h which is the ‘picture’ with respect to the ‘contrastive’ index set. The present design is minimal...

i.e. Bx M ® {i<a} h = {i}1 ą {i}2’ H = {i}1 {i}2 … set S’ is open, with respect to a,b,c, etc.

Î S’. But 1 – n ą S’

How it all is, is a mystery ... and so much for methodology ... this is no principle ... but why this ideology is ideology and revision ... or just functioning ideology, is a mystery and will perforce remain a mystery to methodology and relations.

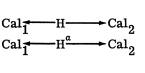
Two Cal’s between which may be found ‘sames’ as to form ‘F’. Or what, indistinguishable? Iterative items, or what? ... There are other possibilities. We may say they are not worth the bother vis a vis distinction. They ‘contribute’ one way or another ... they may be just formal/existential. This needs looking at ... they may not be guessed, just recorded? Anyway, on we go to ‘contribution’. Now, common features are accessible in the hybrid, i.e. go through the list ... and find these links, or fragments ... is that it?

The intermediate form of the hybrid ... this isn’t state, is it? It must be wave like ... This is the ‘dynamic principle’ aspect/the go-on aspect – or is it? Do we note the former and press-on with the latter?

While hybridization is indivisible, it is present in one of n and only n modes ... is this 2? Oscillations of, in or out of phase ... no, these sets are daft; we need it more comfortable. How about a phase picture? That’s computable. Zero scope sames ... are in phase. Non-sames are out of phase. Now, this is not just ‘commonality’ is it?

Now, this needs looking at. Property is merely thought of as functionality. So we have sameness and non-sameness ... formal of just AL dynamic ... entry sameness, or what with respect to going-on? You can have quite a list:

When Cal1 has both surf-scrutiny and function (D) scrutiny and Cal2 has similarly surf and D. When 3 obtains, so does 6 (in the Bxal By Cal forms). Given concatenation/hybridity, which is single and indivisible, it is in the in phase mode between surf and surf, and at the same time in the contrasting (out of phase) mode between D and D, or it is in the converse mode.

The procedures of analysis/understanding involve two separate kinds of factors: a) the materials of a given state of discourse; b) the operators – no?

So, in concatenation, we have no choice but to confront each concatenatum with each other one ... and find the one ‘bond’ hybridity between two boundaries over and over in each separate confrontation. Now what? After a few pages of (mad) digression ... hybridity may have to be tactical ... a reinterpretation of a list: stairways of index sets – Darwinian descent.

A ® B – M is true structure. {[A] ® [B]} . But we want an interpretation for {A} ¬ H ® {B} Cal. (What C. Smith suggested vis a vis transitivity?) Is it sufficient to have a guess principle? Are inter-list relations decidable? Finding a hybridity with respect to concatenation ... this might be a question of degree ... also offer R. Itself. Compatibility. A principle allowing filtration of a kind. The hybridity exists where? An address to the ‘same’ problem ... we can express zero hybridity – but what about ‘low’ epistemic access? There should be a way to avoid infinite hybridity. But expression of epistemic weakness would do. The H is an index with respect to the higher order list... a universe of non-discourse. In what ways can we talk of (epistemic) access? Unless you are dealing with it as prima facie, ‘everything becomes message (at least as asymptote of noise)’. Epistemic weakness might be expressed by H/ – H. It’s all still an index of everyone’s interests-imagination; there are no ‘counterfactuals’.

You would find that concatenation is structural, but it’s also resonance – that is, it’s seldom, if ever, Bx ® By Cal. In fact, it may have to be Bx ® By Cal (so two lists perhaps). A concatenatory unit, the inside structure of which is mesomeric – express that in an alternative list.

From the point of view of resonance this may amount to no more than a semi-structural conjecture. This would make hardly any difference for a workable formalism (plus recognition of a limit). The question of bindability – morphisms just won’t work in the absence of an ‘ortho’ approach. So, what is a possible ‘resonance’? Interpretation? The H is then a ‘unifying’ view – a weakening? A single concept into which the pertinent features of both entities are incorporated? Now, it’s a question of reading-off. But what? Just a unity guess (... this is why Mx/Phil. is right about going-on ... the boundaries ... out-of-the-blue). But we can’t just ‘weaken’ the typology – is it a truism to say of any ‘structure’ that it’s a true structure (from a list)? Compare the concatenata!

Concatenatum: should there be any information as to type? It’s not just type that counts; in fact the information must be restricted to the ‘interiority’, so to speak, of the concatenatum (although we’re dealing with a point of reference and not space). What we could try to set up is a form of hybridity. This is a question of a more elaborate hybridity structure (don’t fear a precluded set – this is just the possibility of a set/data). So we have to get hybridity in the lists. Do we say whether they are the same or not the same, i.e. substitutable or contrastive? You could arrange suitable categories, i.e. 42 lists and then possible ‘groupings’ classification – a propos the Zurich ‘guessing show’. The other thing would be to sort out hybridity ‘later’. How do you do this – and what are the sets involved? It’s just that the expressional possibility might be ‘richer’, and this must rely on a sort of hybridity. Same ... with respect to what? So as to get the resonating situation ... we also have ‘slightly’ different issues ... the logic/the hybridity exists insofar as we deal with ‘present’ possibilities, in expressions ‘for’ ... the concatenation occurrence ... its properties. The R is between sets ... but this is well away from ‘explicit’ hybridity. Is it just a question of ringing the changes on the lists?

Lines and prisms ... what else can one get it to say? ‘It’s the same conversation’ is no good. We want more of a resonance ... how about working it out as a kind of anamorphism? A late concatenization? And then there’s the problem of modalities ... spaces. So far, we have just a property ... don’t we? Confront every item with every other ... this is a question of working out resonances/vibrations.

n Bxal By Cal ... Cal. Properties have to be sorted out somewhere. Determine the property of M, or N’s going-on, or being a going-on relation of some kind. B was ‘blurt’.

‘Mere’ resonance, surely to God ... a structure ... with contributing members ...

A pattern of complementary distribution may or may not emerge; the operator can, presumably, set this up. We need a near ‘complete’ permutated list. Anyway, go-on with the hypothesized ‘sameness’.

There are aspects of formal difference – do we have to see that (for ‘=’)? There are concatenatory componential features in common.

Now, can we consider that there is no contrast with respect to the items’ being functional signals? But functional property is ‘same’ or ‘not-same’. Is that just agree/disagree?

An earlier datum –

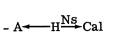
B. Now, can we postulate a rule of congruence? The resonance is between operators ... or between Art and Languageists – participants (as operators of M). Does this suggest any ideological revisionary true structures? This is a question of the incorporation of pertinent common features ... of concatenatory properties... What’s the answer? A rule of congruence would suggest that:

We can’t just have that sort of comparison; there may be other approaches. What we want is cyclical output.

We still have to investigate the possibility of encountering other I – like concatenatory events, and their possible incorporation as to going-on into I, i.e. as contributing members. I (an ideological concatenatory possibility) might be defined as a true structure the expression of reverberation between related items in (on) the A & L discourse map. Is this as anyone wants it? However, concatenatory events of a similar type do recur ... they can be regarded as contributory in some way.

According to the theory (quasi-theory), the patterns of distribution of concatenatory (grammatical) occurrences is statable as follows:

There has to be a further adaption.(SIC) Where is the typical hybridity? When and where it is typical may be too stupid/complex for us to understand.

And, however,

is the use of a hybridity out of court.

We should continue with the ideas about the sets. There’s some basis for using concatenation. So: C set , plus usable indices. Anaphora indices are fairly minimal with respect to power. ‘Hello H’, said Terry: C1 H C2.

The congruence problem – this may be a question of finding an analogue of the two hybridity planes. Coincidence with ‘their’ chat – a chance to modify the generatum of the grammar. We can postulate a ‘weakness’ somewhere, or perhaps a ‘vast’ or infinite resonance. Expression and ideas is all too silly. But you’ve got to reach some sort of analogue ... at least is it between ... discourse and universes of sets of discourse.

Cal... B, etc. ... with suitable indices. Let’s try out some modification on the operations. The indices can’t be too behaviouristic. It can’t be just about form and content. We could postulate a hybridity with ‘content’ – topic significance. And ideology – to show a possibility of ideology – our language (cf. Hegel). Take a part seriously ... just a pathway won’t do ... It’s got to grow (that is to say we can’t slot in an independent result).

Might we just have no surface? A transformationally filterable surface? This is to say a filter concatenation ... or an ideological measure thereof – the possible relations of a range of several expressions. Ideology is not just ‘attitude’ or point of view.

This can be no less than concatenation. Now, back to the problem of the sets. Stress and syntactic ... transformations...

Our categories are not sets of expressions – but instead they serve as indices (of what axes?). The set of discourse items is to be the smallest set X such that Cal1and Cal2 are in X. Another issue:

whenever a and b are in X... etc. (Montague).

The going-on function – we need more structure.

Cal ® as categories.

We don’t really have a basic set of expressions at all.

A set of basic teleological categories? Rehearse operator teleologically. An r ... they say if they are ‘same’, they create the hybridity. That’s easy ... they can use consistent lists. If you can set up hybridity, there must be a congruence.

But one does want the hybridity. Can it be in terms of form and property? Surely not form corresponding to that which amounted to a point of reference/a ‘way of life’ set bounded just by description. It’s still a question of building-up a picture ... but we don’t have to take the ‘findings’ seriously. (Consider the G. Sperone form-filling situation!)

We can set up the concatenation list ... as a grammatical possibility. It can’t be just a tactical issue we’re dealing with.

We could sort out a set of conditions that would make us think of concatenation ... going-on as a popular fallacy. The effort must be to produce a logos situation ... where chat is chat...

Indices ... not just synoptic indices ... further activity is necessary – a) (F) H can be H i ‘same’, or you can have b) (F) h where i ‘contrasting’, and at the same time you get for a) a ‘contrasting’ and for b) a ‘same’. Is this at all necessary now? That would just alter interpretation wouldn’t it? Change the category perhaps? ‘i’ can, so to speak, ‘explain’; ‘a’ has to be a dummy. There is index set congruence – in that case it ‘has to be’. It’s just a recondite publishing of results. If you’ve got an F ‘contrasting’ and an i ‘same’ and a Bxal ‘contrasting’, you’ve got to have a ‘contrasting’. O.K.

Now for P’s. The same follows with respect to congruence and also ‘inside’ congruence, i.e. where you get P ‘contrasting’, you get H ‘same’.

So this is the first two stages for IBMR and the time? It’s still guessing.

Now for the congruence breakdown. Anything with anything. Should that be left as a problem? No, but that is on the form – surely index congruence will hold it together. But why compare? Is it just a weakening or what? No, it’s a new hypothesized concatenation ... saying not a lot.

That’s not too bad. The more ‘internal’ congruences are Cal in a way. They have the text cardinalized. There is always problem-solving. How can the sets be preserved or found? The non-congruent thing is i set addition. But that’s far-fetched ... T. M. Cheng ... what we have is a piece of going-on assembled... Could we have a chain? All this presumes synchronic/diachronic thinking.

And here you’d have an H° that results in a straight C, except for the fact that the structural relation TAMB « IBMR is hybridized by its being missed by TAMB. So H° is a form of Cal – but {i}, {b} get in on the act in a ‘contrastive’ way – as a ‘boundary’ comparison.

You note, in other words, h° and h°.

Next there’s H°°

Now this is {i}, {b} coming home to roost. H°° says {i}1 = {i}2’ therefore {b}1 ą {b}2. h°° conversely

The dummy index needs to put through fairly arbitrarily – ‘sprinkled’.

H°° = anything and anything + congruence.
H°° = ... + congruence.

Brainstorm Proposal

A-H – a natural numbers series and given; 1-7 – concatenations – closed set (?); 1/2, etc. – of an open set (?).

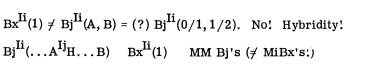
Apropos (...A.. .Hi.. .B...), fuck Zeno’s paradox, or any other paradox.

1) Bx(1, 2) e Ii and Bx(3) Î Ij: there is a set of conditions for a grammar of (1®3®...) as a set system I indexed a posteriori from i-n, and so (1®3, etc.) is ‘frozen’ at II.

2) Bx = a wff, closed set; Bj = an open (wff?) set and is a function of revision on Bx, i. But to the extent that (1) ą (A, B)? would be a silly question.

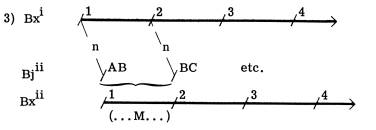
4) Revision on the Bx grammar is such that any Bxi / Bji ą, but Bji =/= MBxi; and ‘revision’ is Bxi ® Bxjxi (...H...)xj. MM {Bx ® Bj} = Bj ® MBx. That is, the architectonic is a product of the M of experience from both the indexing of a cluster to a (unhappy) Naturlogik continuum and as an historical-cultural phenomena as instrumentality.

Figure and ground/horizon – point of reference and point of focus-drill and learning.

How could Bx nest in Bj? It couldn’t since (or it’s trivial that it do.....) Bji (1) has no set conditions save for Ii(1) ... otherwise it’s Ii(Bx, 1), etc.

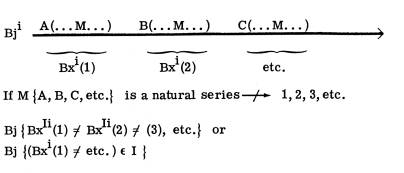
But ‘A (... M... ) B’ as a brainstorm proposal?

Nesting might take place along the Bj axis to provide a Bx wave ...

‘MA, MMB...’? (MA(MA, MB)(MA, MB, MC)).

But this nesting can only be truly transformational, i.e. unrecognizable and unknown/unmappable, unless any conversation was, roughly, something like “‘surf’ “‘surf’ ‘surf””’, etc.

Bj as vector, but without magnitude; not even the kinematics of a rigid body (structure); just the M of an -emics? Graphics is a fragment of that problem. But you can just tell someone that Bj is an unbounded field even when it’s ÎIi. But that’s making vectoral assumptions about the Bj mapping. Not quite, since it might be ‘frozen’ outside any lattice for Bx, and beyond the reach of any neighbouring Bj.

The ‘disjunctioning’ (of the ‘surface’) for Bj is ‘Bj(1) ą Bj(2)’ – and as the field is ‘n-dimensional’, then ‘Bj(1) = Bj(2)’ will have to be rewritten in scalar form/‘structure’.

N.B. if Bj(1)a ą Bj(2)a, then set conditions aren’t just surface, i. e. if a = a list to be run up for all rational/cardinal continuum, (1) a = U for all i’s in I; and that’s a funny way of going about constructing a pragmatics.

And for any ordinal ‘series’, a = -M of (1)a for any i = (1)a for any other i: Bj (1) ą Bjt (i).

And you can’t say that BjIi (l) is an open set, or rather a member of an open set which has only one member – re rules of congruence. (But it has at least more than one member.) Magnitude is then encapsulated in Bx prima facie mappings and dialogical strengths. The set Bx-ing is an historical continuum of an ordinal series where each ordinality is ‘(x)BjIi’. That’s back to Bj = M of Bx: the latter can describe a wave and the conditions for the vectoral ‘pattern’ and M dynamics for that wave – a clustered, open/but (naturally) numbered/historicalBj’s.

For set Bj it has no, can have no, sense save as an historically (pseudo-) ordered point of reference in a dialogical set.

‘Learning’ as a Bj function on an n-series (Bx-ing=wff I) – (as still asking the question) not a mapping? a) There’s no qualitative/scalar difficulty in embedding x and y. b) But without direction?

Bj’s aren’t in any set ... There can’t be any series except in a natural sense as an uninterpretable string. A series has direction anyway.

‘1(Bj)2(Bj)3... etc.’, ‘Bxl(Bj)Bx2(Bj)Bx3... etc.’

But if every function-modality of any point of reference contains all the functions of every other point of reference and can generate them Turing-style then ‘1(Bj)2(Bj...’ isn’t a series ® and whither BxBj ? Unless it’s BxlBx2, etc., etc....

But (...A...) and (...B...) Î Ř, i where Ř i = what?, where?, when?, etc.; in brackets?

Inter-set Bj1 = Bj2? Only to the ‘natural ontic elements’. Or this identity is of a non-finite possibility of the possibilia of experience, i.e. a finite fragment of the immanent n-indexing which is not (merely) transformational to any part of discourse, i.e. the generating aesthetic.

R1. BxIi(1) = BxIi(2) : BjIi(1) ą BjIi(2) for closed and wff sets, Î U, interpretation: agrammar.
R2. Iterations of I’s (a, b, g, d, etc.). Anti-anaphor/surface trap: BxIi(1)a ą BxIi(1)b
R3. Rewritting: BxIi(1)a = BxIi(2)a Bx(1)a = / >By(2)a

But - there is M of Bx-tactics from the margin of Bj – wave mechanics.

Bj (1)a ą Bj (1)b intra/sub-set ... neighbouring Bj(1)g etc.

Focus on Bji with (simply?) ‘repeating’ ‘going-on’, the blurt and drawing the quasi-continuum/life-restrictions ‘< >‘ – what would you get? Only an iterated range of series dependent upon the-defeasible-conditions-of-that-range. Anyway, since its character is ‘revisionary’, you can’t map it, only experience it ... unless ‘some a’s are b’s’. But consider ‘(…)’ in (...A) as conditions for a mapping, outside iterated, ‘closed’ and open sets. It’s not:

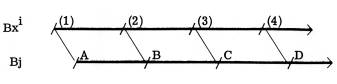
or Bj (1, 2; 1, 2, 3; ... etc.)C.

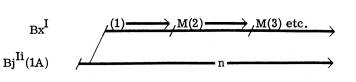
BxIi (1) < BjIi (...1a) = Bxa1 By Cal e (grammar), e = {Bj CBK} Î revisioni…

But – revisioni is of M of BxIi (l) ą BxIj (1), not of BjIj (... 1).

R4. An infinite set with no recursively countable set with immune complement is said to be simple (i.e. we might – naturally – be able to deal with it).
R5. Immune sets aren’t productive (as mapping), i.e. immune = n + i (plus nj but going-on).
R6. Hence Bj(...X...)®(Bi) = creative sets. But we’re not dealing with a ‘consistent theory’, but of finite length – No! – but consistent because of infinity and therefore immune from (sets and subsets = defence).
R7. A Ł B if A is recursive in B, i.e. if therefore that’s not just A Î B? A trivial function CA(X) vanishes if and only if x Î A, then generated from CB(X).

Bx Ł Bj ® however for any Bx-ing.
Bx Ł Bj: but CA (x) depends upon a chain strength between A and B.

Bxi (1) = Bxi (2); but (Bxi (l))Bj ą (Bxi (2))Bk.

Answering a question satisfactorily isn’t stopping the dialogue ... or hiatus ... rather than M of immune set-theoretical conditions for treating Bx By Cal, i.e. the old model of Bx is satisfied if and only if By lets him/it =

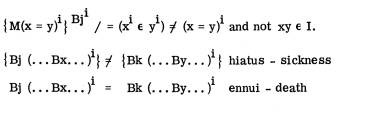
‘Revision’ is scalar, R to I.

Revision/Bj is immune to any of its subsets. So that the ‘whole’ of the ‘reflexive, non-specific pragmatics’ has any fragment that is R to Bj? Bj, Bk is not productive complementarity – is not regenerating the (depth ® M of surface).

Revision/Bj is (perhaps) a classically ‘simple set’, although Bj might be transformed into a productive non-finite string – into Bx – which is not a non-finite string.

But Bx ^Đ Bj if any function/modality of Bx can be generated from Bj ... (Bx)Bji is not recursively countable – ‘simple’; Bx is our weakness for dialogical satisfaction – if it weren’t that, Bx would be ennui. Anyway, Bx is immediate erotetic satisfaction, which is as absurd as stopping the conversation.

Immunity ą (Productive mapping, i.e. a continuum). Its only spectre is the ‘triviality’ of extrapolating – from the nesting – the continuum.

Ask questions about Bx and – christologically – you get a partial mapping of Bj -(U1…(U2…(U3…))), etc. only if Bj was a generative quasi-base.

Continuity of non-iteratable (pragmatic) set Bj – as exhaustively immune from Bk – is either an iteration of the set-conditions of Bj’s, Bk’s strength or ironically their completeness.

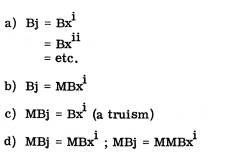
The ontological problem: if Bj accelerates from Bx, then the ontological/methodological problems that accrue from Bx-ing, are articulated as:

$(Bx) Î all M’s of ($x).

But that’s not a different type-ing between Bx and Bj.

Ontological problems of the margin®perhaps like this ...

An event ‘X’; lived through XiM*®and mapped Bxal;

Bxal ą XiM / ą ‘X’

‘X’ does not accelerate away from Bxal.

XiM = Bj > ‘X’ /® Bx

And it’s not Bj(. . .Bx...) is it?

No? Well, because of the algebraic possibilities of Bj – they can in no way be brought out of the plane of Bx.

N. B. vector without magnitudes, e.g. 1, 2, 3, 4... is not a continuum unless 1(®) 2(®) 3(®) etc… where ‘(®)’ is common to all numbers. That’s an ontological problem … if (®) is common to all, i.e. common to a set … Anselm: there’s no difference between 1, 2, 3, and 4, etc. … if 1, 2, 3, 4, etc. belong to a set (counting numbers). There’s no scale, magnitude without M vector.

N. B. (…3…)
‘3’ = an historical point of reference; but the vectors’ values for ‘1’, ‘2’, etc. are not identical, save at L.C.D.’s.

That’s an historical problem of arithmetic ... It’s also a problem of varying and grouping modalities/arguments. For example, Ml®M2®M3 approaches a grammar /epistemological plane which it can describe ... reflexively and elliptically.

Ml®M2®M3 must (?) be in some relation to the reiteration of that continuum.

There is a relation between Ml and M2 other than concatenation. O. K., there’s no hierarchy between Ml and M2 in a set (...M1 and M2 and...), but between (Ml)1 and (M2)2.

Hierarchy can be as simple-minded as (Ml)1® (M2)2, etc. etc.

Back to a series, 1, 2, 3, etc.

(“‘Resignation’M1’ ‘String’ M2’ ‘Drill’ M3 ”)i

(“‘Ideology’M1’ ‘String’ M2’ ‘Drill’ M3 ”)k

a) (M1®M2®M3…)i
b) (Ml, 2, 3)i® (Ml, 2, 3)k
c) (Ml)i®(Mi)k®(M2)i®(m2)k

a) Intra-set relations as a problem of continuity.
b) Inter-set continuity problem.
c) Inter and intra-set continuity and possibility of a ‘grammar’.

Continuity and ‘margins’: if the margin is only an arbitary (pragmatic) finite limit of the soul contents, then continuing the modalities of the soul is non-problematic; and the relationship between the modalities is non-problematic ... rather than recognizing the ontological bifurcation between margin and existence, i.e. (M1…M2…M3…)i, i.e. Bj ą (Bx + N…+…)

BxBj ą Bj as a parameter/discrete edge, although it is a function.

‘Negative Feedback’

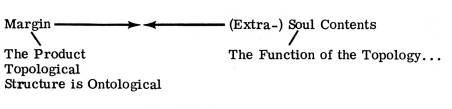
Continuity/Going-on ... and change ...

The constructivistic root leads us to rational numbers = natural numbers = real numbers ... all counting is non-different:

[1, 1(2), 1, 2(3), 1, 2, 3(4), etc.]

Otherwise we do face the Zeno paradox with a ‘rational change of belief’® (non-Bayesian, non-utility learning) ®
a) We’d have, in changing from Bap® Baq, p as non-rational and q as rational. Why was p = rational? Why is q rational?
b) How does a rational change take place if pR and qR and – (p and q) R?
c) Zeno: pR1…qR2 and R1®R2 or ‘Rl and R2’ along with Rn and R2 so that pR1 ..pRn...pR2. Don’t bother with p’s and q’s – it’s not propositional ... so change is not diachronic.
d) Change as revision (complete (= all the M’s of R1 are members of a set R2 with or without the a priori weights attached – at least they are ‘described’ – taken care of – iterated – in R2)).
e) ‘Rational change’ would be the grammatical in the Bxal sense, i.e. it would be a state description of what happened when ‘Rl®R2’/ ‘Rl and R2’ was suspended in its own incomplete M’s (although ‘Rl and R2’ might be complete?), i.e. the rational change is the M’s of change in a continuum ‘Rl, R2’, not from R1 to R2 / R1®R2!!

Therefore, M ‘Ra®Rf’ is a rational change ... ‘it depends how low we stoop for our rationality conditions.’

N. B. ‘Bxal By Cal’ is,as a rational change, incomplete because of the M’s of interpreting the state descriptions, and that equals M’s of Bj ... Therefore, we must discuss rationa.l change – it’s just an index of Bj.

Change and Dialectic

Hegel – Natural Discourse – Synthesis – Naturlogik ... But the Reich des Sollens – Sickness unto Death – The Absolute Final Conclusion – i.e. the total and finite solution of Hegel’s logic – what arises from Hegelianism is a peculiar type of problematic.

And but again®absolute idealism (etc.) as ideology as a weapon. (O. K., bring in Bayesian utility there ...).

Bj > the Reich des Sollens – Hegelian disjunction. Change is chronic not diachronic ... and wff (as nature).

1(…M…), 2(…M…), etc. plus ‘1(…M…)i, … 2(…M…)j … etc. “hiatus point” … 3(…M…), etc. ‘as wff, i.e. ‘going-on from memory’, ‘where left off last week’.

But ‘(1, 2, 3...)BxalBj’ is not a hiatus point. Except for Bx ... for Bj it’s finished ... and wff complete.

A series of NN = a M (set of) state description(s) which ‘X’ is unable to understand as coherent: this is a lattice-mapping remark... it’s coherent as a series, but not as a congruency to ‘Y’s’ series.

{ 1, 2, 3}Y
{ 1…2…3…etc.}Y

(Rules of congruency, M of a critique of a NN series.)

Learning?

‘Escaping from uncertainty’ vis-a-vis NN series as ‘iterated rational strings’?

M of learning as pattern recognition, i.e. Bx-ing towards a partial grammar of a function ... given that as learning with a Bayesian utility principle(s) – N. B. Harold’s retrospective ‘rejectamenta’.

… How the Bx-ing could treat it (modalize it) would thus be a function (trivially) of how the ‘rejectamenta’ (anything Bx-ed) be ‘seen’

... But how does anything Bx-ed get seen/viewed in relation to Bj’s? Could be ‘Bj and Bx’ (as the margin capturing the soul – an absurdity as a subset, but an implication of the Quinean, Draconian ontology).

Therefore determinism and anti-determinism?

The intractability of vectors comes from the absurdities (involved only in the nexus of phenomenologies dealing with data) of characterizing the kinematics of a rigid body with the inertia (modalities) of a system of (linguistic/‘concrete’?) particles.

Ontological fast-breeding of i’s is not a problem – escaping from vicious localization of i’s (as an approximate of an epistemological situation) which may (?) catch up with localized ellipticality ... which may be the problem to approach apropos the (any) ontological intractability.

That is, set inclusion, with, at best, a list of modalities (without priority).

Would the following Bx/Bj provide no complexities of an aggregating Bj set – i.e. forgetting/memory?